Tutorial 5 - Dynamic Solution Methods¶
Introduction¶
In the previous tutorial we discovered the general structure of the PyMacLab DSGE model instance and saw how this programming approach lent itself well to the idea of inspecting and exploring the instantiated models’ current state, summarized by its data fields and supplied instance methods equipping them with functionality. This section finally discusses how the library equips DSGE model instances with methods which make use of the models’ computed Jacobian and Hessian, which are evaluated at the models’ numerical steady state. As a short reminder, we may recall here that it is often this step of obtaining a steady state can prove difficult in the case of a number of well-known models. Notwithstanding, for the remainder of this section we will assume that a steady state has successfully been attained and that the model’s Jacobian and Hessian have been computed. Let’s first start with our usual setup of lines of code entered into an IPython shell:
# Import the pymaclab module into its namespace In [1]: import pymaclab as pm In [2]: from pymaclab.modfiles import models # Instantiate a new DSGE model instance like so In [4]: rbc1 = pm.newMOD(models.stable.rbc1)Since we have not supplied the instantiation call with the initlev argument, the model has been solved out completely, which includes the computation of a preferred dynamic solution, which in the current library’s version is Paul Klein’s 1st-order accurate method based on the Schur Decomposition. This means that one particular solution - if existing and found - has already been computed by default. Readers familar with this solution method will know that this method requires a partitioning of the model’s evaluated Jacobian into two separate matrices, which for simplicity we denote A and B. They are computed by default and are for instance inspectable at rbc1.jAA and rbc1.jBB.
The Jacobian and Hessian: A Detour¶
One of the great advantages of PyMacLab is that the Jacobian and Hessian are NOT computed or approximated numerically using the method of finite differences, but are calculated in exact fashion analytically using the special-purpose Python library Sympy, which is a CAS - or computer algebra system, similar in functionality to Mathematica and Maple. You can inspect the analytical counterparts to the exact numerical Jacobian and Hessian which have not yet been evaluated numerically at rbc1.jdicc and rbc1.hdicc, where the latter reference actually refers to the 3-dimensional analytical Hessian. If the model is composed of n equations describing equilibrium and optimality conditions, then the Jacobian is made up of
elements and has dimension
, because the derivatives are formed not only w.r.t. to current-period, but also future-period variables. Equally, the Hessian is a 3-dimensional matrix of dimension
[1].
Notice that for the numerical counterpart to the 3-dimensional Hessian, PyMacLab instead uses an alternatively dimensioned version of dimension
, which is the Magnus and Neudecker definition of a Hessian and is useful when one wishes to avoid using matrices of dimension larger than 2 and the corresponding Tensor notation. Again, you can exploit PyMacLab’s DSGE model instance’s design in order to inspect the derivatives contained in the Jacobian and Hessian inside an IPython interactive shell environment, such as follows:
# Import the pymaclab module into its namespace, also import os module In [1]: import pymaclab as pm In [2]: from pymaclab.modfiles import models # Instantiate a new DSGE model instance like so In [4]: rbc1 = pm.newMOD(models.stable.rbc1) # Check some elements of the analytical Jacobian and Hessian # Jacobian, equation 3, derivative w.r.t. k(t-1). Notice that Python arrays are 0-indexed. In [5]: rbc1.jdicc[2]['k(t-1)'] 'rho*exp(z(t))*exp(k(t-1)*rho)' # You could also retrieve the evaluated equivalent of the above expression. # Here you need to know the position of k(t-1) in the ordered list of derivatives, you can check # that k(t-1) is on position 5 by inspecting rbc1.var_li In [6]: rbc1.numj[2,5] 1.3356245171444843 # Hessian, equation 3, 2nd derivative w.r.t k(t-1). In [6]: rbc1.hdicc[2]['k(t-1)']['k(t-1)'] 'rho**2*exp(z(t))*exp(k(t-1)*rho)' # The numerical evaluated equivalent can be retrieved as well. # We are not retrieving the above value via rbc1.numh[2,5,5] as we are not working with # the usual 3D notation of Hessians, but with the Magnus & Neudecker 2D definition of it. # The result is correct, as the 2nd derivative is just rho(=0.36) times the first derivate. In [7]: rbc1.numh[21,5] 0.48082482617201433Now we have explored the ins and outs of PyMacLab’s way of handling the computation of a DSGE model’s Jacobian and Hessian. Equipped with these building blocks, it is now time to move on to a discussion of the actual solution methods which PyMacLab provides by default.
Dynamic Solution Methods - Nth-order Perturbation¶
Solving nonlinear rational expectations DSGE models via the method of perturbation represents an approximate solution around the computed steady state of the model. Since this approach is not too dissimilar from a Taylor Series expansion of a function around some point students learn about in some 101 maths course, it should come as no surprise that here too 1st and higher-order derivatives are needed in order to arrive at solutions which increasinly reflect the true exact solution of the system.
PyMacLab offers methods suitable for computing such approximated solutions based on linearization techniques which can either be 1st- or 2nd-order accurate. In order to obtain these solutions, we make use of Paul Klein’s solution algorithms, which are available on the internet and have been incorporated into PyMacLab. Needless to say, Klein’s 1st-order accurate method using the Schur Decomposition has been around for a while and only requires knowledge of the models Jacobian, while his latest paper (co-authored with Paul Gomme) spelling out the solution of the 2nd-order accurate approximation, also requires knowledge of the Hessian.
Choosing the degree of approximation¶
At the time of writing these words, PyMacLab includes full support for both of these two methods, where the first method has been made available by binding Klein’s original Fortran code into PyMacLab and making it accessible via the node rbc1.modsolvers.forkleind which provides the solution method callable via rbc1.modsolvers.forkleind.solve(). Once this method has been called and a solution has been found, it is essentially encapsulated in the matrices available at rbc1.modsolvers.forkleind.P and rbc1.modsolvers.forkleind.F, which represent matrices of dynamic elasticities summarizing the optimal laws of motion for the set of endogenous state and control variables, respectively. Since this method is actually internally calling a compiled Fortran dynamically linked library, its name is prefixed with for.
Klein & Gomme’s 2nd-order accurate method uses the solution from the 1st-order accurate method as a starting point but in addition also makes use of the model’s Hessian and the information provided by the model’s shocks variance-covariance matrix, in order to produce solutions which are risk-adjusted in some loosely defined sense. This solution method therefore no longer displays the well-known property of certainty equivalence for which first-order approximations are so well known for. At the moment, this solution method is completely implemented in the Python language itself and is callable at rbc1.modsolvers.pyklein2d.solve(). As already mentioned, the method makes use of rbc1.modsolvers.forkleind.P and rbc1.modsolvers.forkleind.F, the variance-covariance matrix rbc1.modsolvers.pyklein2d.ssigma, and the Magnus & Neudecker definition of the Hessian rbc1.modsolvers.pyklein2d.hes. It’s solution is encapsulated in the following objects:
Object Description rbc1.modsolvers.forkleind.P Matrix of elasticities describing optimal law of motion for endog. state variables, 1st-order part rbc1.modsolvers.forkleind.F Matrix of elasticities describing optimal law of motion for endog. state variables, 1st-order part rbc1.modsolvers.forkleind.G Matrix of elasticities describing optimal law of motion for endog. state variables, 2nd-order part rbc1.modsolvers.forkleind.E Matrix of elasticities describing optimal law of motion for endog. state variables, 2nd-order part rbc1.modsolvers.forkleind.KX Array of risk-adjustment values for steady states of endogenous state variables rbc1.modsolvers.forkleind.KY Array of risk-adjustment values for steady states of control variables Once the above mentioned matrices are calculated, the solutions to either the 1st-order or 2nd-order accurate approximations are available and can be used by researchers to compute (filtered) simulations as well as impulse-response functions in order to either plot them or generate summary statistics from them. Luckily, neither of this has to be done by hand, as simulation- and IRF-generating methods are already supplied and convenience plotting functions are also readily available. But this will be the topic of our next tutorial in the tutorial series for PyMacLab.
Footnotes
| [1] | Obviously, we are abusing clearly defined mathematical definitions here to some extent, as a classical Jacobian would be
of dimension 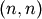 and a classical Hessian of dimension and a classical Hessian of dimension 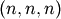 . The only reason
why here computed dimensions tend to be twice as large has to do with the fact that for Klein’s first-order accurate solution
method we require knowledge of derivatives w.r.t. both current and future (expected) versions of the set of all variables. . The only reason
why here computed dimensions tend to be twice as large has to do with the fact that for Klein’s first-order accurate solution
method we require knowledge of derivatives w.r.t. both current and future (expected) versions of the set of all variables. |
