Tutorial 5 - Steady State Solution Methods¶
Introduction¶
In the previous tutorial we learnt how a PyMacLab DSGE model instance possesses the capability to intelligently upate its properties following the re-declaration at runtime of attached data fields such as the parameter space or the set of non-linear first-order conditions of optimality. In this section we will learn an important component to PyMacLab’s DSGE models which provides users with a large number of options available for solving models’ steady state solution. The great number of possible avenues to take here is quite deliberate; it would be reasonable to argue that for medium- to large-sized models the most difficult part to finding the general dynamic solution based on the approximation method of perturbations is to first obtain the steady state solution around which the approximations are computed. In total we are going to explore 7 different variants suitable for seeking to compute the steady state. So let’s get started.
Option 1: Using the model’s declared FOCs and passing arguments at model instantiation¶
Choosing option 1 allows users to leave the numerical as well as closed form steady state sections in the model template files entirely empty or unused indicated by the “None” keyword inserted into any line in these sections. In this case, the library has to rely on the time- subscripted non-linear first-order conditions of optimality, convert them to steady state equivalents and somehow discover the required set of initial guesses for the variables’ steady states to be searched for using the non-linear root-finding algorithm. This is accomplised in the following way. Consider first the following simple example of a DSGE model file:
%Model Description+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ This is just a standard RBC model, as you can see. %Model Information+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Name = Standard RBC Model; %Parameters++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ rho = 0.36; delta = 0.025; R_bar = 1.01; betta = 1/R_bar; eta = 2.0; psi = 0.95; z_bar = 1.0; sigma_eps = 0.052; %Variable Vectors+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ [1] k(t):capital{endo}[log,bk] [2] c(t):consumption{con}[log,bk] [4] y(t):output{con}[log,bk] [5] z(t):eps(t):productivity{exo}[log,bk] [6] @inv(t):investment[log,bk] [7] @R(t):rrate %Boundary Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variable Substitution Non-Linear System++++++++++++++++++++++++++++++++++++++++++++++++ [1] @inv(t) = k(t)-(1-delta)*k(t-1); [2] @inv_bar = SS{@inv(t)}; [3] @F(t) = z(t)*k(t-1)**rho; [4] @F_bar = SS{@F(t)}; [5] @R(t) = 1+DIFF{@F(t),k(t-1)}-delta; [6] @R_bar = SS{@R(t)}; [7] @R(t+1) = FF_1{@R(t)}; [8] @U(t) = c(t)**(1-eta)/(1-eta); [9] @MU(t) = DIFF{@U(t),c(t)}; [10] @MU(t+1) = FF_1{@MU(t)}; %Non-Linear First-Order Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++ # Insert here the non-linear FOCs in format g(x)=0 [1] @F(t)-@inv(t)-c(t) = 0; [2] betta*(@MU(t+1)/@MU(t))*@R(t+1)-1 = 0; [3] @F(t)-y(t) = 0; [4] LOG(E(t)|z(t+1))-psi*LOG(z(t)) = 0; %Steady States [Closed Form]+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Steady State Non-Linear System [Manual]+++++++++++++++++++++++++++++++++++++++++++++++++ None %Log-Linearized Model Equations++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variance-Covariance Matrix++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Sigma = [sigma_eps**2]; %End Of Model File+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++Notice how we have left the usual sections employed to supply information useful for finding the steady state unused indicated by inserting the keyword “None”. As you can see by inspecting the system of non-linear first order conditions, a steady state could be obtained by passing a steady state version of the FOCs to the non-linear root-finding algorithm, with the additional qualifier that in this particular case we would ideally like to omit passing the last line which is just a declaration of the own-lagged law of motion of the exogenous state [1] productivity shock. This would lead to a 3 equation system in c_bar, k_bar and y_bar. Further more, we would have to let the model somehow know the set of intial guesses for these three variables, which we often tend to set to some generic values, such as 1.0 for all three of them. How is all of this accomplished? By passing the relevant variables directly to the DSGE model at instantiation time like so:
# Import the pymaclab module into its namespace, also import os module In [1]: import pymaclab as pm In [2]: from pymaclab.modfiles import models # Define the ssidic of initial guesses or starting values In [3]: ssidic = {} In [4]: ssidic['c_bar'] = 1.0 In [5]: ssidic['k_bar'] = 1.0 In [6]: ssidic['y_bar'] = 1.0 # Instantiate a new DSGE model instance like so In [7]: rbc1 = pm.newMOD(models.stable.rbc1_ext,use_focs=[0,1,2],ssidic=ssidic)The default value passed to the DSGE model instance’s argument “use_focs” is False, the alternative value is a zero-indexed Python list (or tuple) indicating the equations of the declared system of FOCs to use in finding the steady state numerically. In the case of the model file given here, we don’t want to use the last line of 4 equations and thus set the list equal to [0,1,2]. We also define a dictionary of initial starting values or guesses for the three steady state values we wish to search for and pass this as a value to the argument ssidic. This method has the added advantage that steady state initial starting values can be determined intelligently at runtime external to the model file.
Option 2: Using the model’s declared FOCs and passing arguments inside the model file¶
Choosing option 2 is essentially mimicking the same method used in option 1, with the only difference that everything happens inside the model file itself and nothing has to be passed using arguments to the DSGE model instance at instantiation time externally. Instead, the list of FOC equations to be used in the calculation of the steady states is passed inside the numerical steady states section, as shown in model files rbc1_focs.txt, as follows:
%Model Description+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ This is just a standard RBC model, as you can see. %Model Information+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Name = Standard RBC Model, USE_FOCS; %Parameters++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ rho = 0.36; delta = 0.025; betta = 1.0/1.01; eta = 2.0; psi = 0.95; z_bar = 1.0; sigma_eps = 0.052; %Variable Vectors+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ [1] k(t):capital{endo}[log,bk] [2] c(t):consumption{con}[log,bk] [3] y(t):output{con}[log,bk] [4] R(t):rrate{con}[log,bk] [5] z(t):eps(t):productivity{exo}[log,bk] [6] @inv(t):investment[log,bk] %Boundary Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variable Substitution Non-Linear System++++++++++++++++++++++++++++++++++++++++++++++++ [1] @inv(t) = k(t)-(1-delta)*k(t-1); [2] @inv_bar = SS{@inv(t)}; [2] @F(t) = z(t)*k(t-1)**rho; [2] @Fk(t) = DIFF{@F(t),k(t-1)}; [2] @Fk_bar = SS{@Fk(t)}; [2] @F_bar = SS{@F(t)}; [3] @R(t) = 1+DIFF{@F(t),k(t-1)}-delta; [4] @R_bar = SS{@R(t)}; [3] @R(t+1) = FF_1{@R(t)}; [4] @U(t) = c(t)**(1-eta)/(1-eta); [5] @MU(t) = DIFF{@U(t),c(t)}; [5] @MU_bar = SS{@U(t)}; [6] @MU(t+1) = FF_1{@MU(t)}; %Non-Linear First-Order Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++ # Insert here the non-linear FOCs in format g(x)=0 [1] y(t) - @inv(t) - c(t) = 0; [2] betta * (@MU(t+1)/@MU(t)) * E(t)|R(t+1) - 1 = 0; [3] R(t) - @R(t) = 0; [4] y(t) - @F(t) = 0; [5] LOG(E(t)|z(t+1)) - psi*LOG(z(t)) = 0; %Steady States [Closed Form]+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Steady State Non-Linear System [Manual]+++++++++++++++++++++++++++++++++++++++++++++++++ USE_FOCS=[0,1,2,3]; [1] c_bar = 2.0; [2] k_bar = 30.0; [3] k_bar = k_bar**alpha; [4] R_bar = 1.01; %Log-Linearized Model Equations++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variance-Covariance Matrix++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Sigma = [sigma_eps**2]; %End Of Model File+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Option 3: Supplying the non-linear steady state system in the model file¶
Yet another way available for finding the model’s steady state is similar to the one in option one in that it uses a system of non-linear equations specified in this case directly inside the model template file. The reason why one would want to prefer this option over option one has to do with the fact that the steady state version of the non-linear first-order conditions of optimality can often collapse to much easier to work with and succincter equations which the model builder would want to write down explicitly inside the model file. So this example would be exemplified by the following model template file:
%Model Description+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ This is just a standard RBC model, as you can see. %Model Information+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Name = Standard RBC Model; %Parameters++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ rho = 0.36; delta = 0.025; R_bar = 1.01; eta = 2.0; psi = 0.95; z_bar = 1.0; sigma_eps = 0.052; %Variable Vectors+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ [1] k(t):capital{endo}[log,bk] [2] c(t):consumption{con}[log,bk] [4] y(t):output{con}[log,bk] [5] z(t):eps(t):productivity{exo}[log,bk] [6] @inv(t):investment[log,bk] [7] @R(t):rrate %Boundary Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variable Substitution Non-Linear System++++++++++++++++++++++++++++++++++++++++++++++++ [1] @inv(t) = k(t)-(1-delta)*k(t-1); [2] @inv_bar = SS{@inv(t)}; [2] @F(t) = z(t)*k(t-1)**rho; [2] @Fk(t) = DIFF{@F(t),k(t-1)}; [2] @Fk_bar = SS{@Fk(t)}; [2] @F_bar = SS{@F(t)}; [3] @R(t) = 1+DIFF{@F(t),k(t-1)}-delta; [4] @R_bar = SS{@R(t)}; [3] @R(t+1) = FF_1{@R(t)}; [4] @U(t) = c(t)**(1-eta)/(1-eta); [5] @MU(t) = DIFF{@U(t),c(t)}; [5] @MU_bar = SS{@U(t)}; [6] @MU(t+1) = FF_1{@MU(t)}; %Non-Linear First-Order Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++ # Insert here the non-linear FOCs in format g(x)=0 [1] @F(t)-@inv(t)-c(t) = 0; [2] betta*(@MU(t+1)/@MU(t))*@R(t+1)-1 = 0; [3] @F(t)-y(t) = 0; [4] LOG(E(t)|z(t+1))-psi*LOG(z(t)) = 0; %Steady States [Closed Form]+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Steady State Non-Linear System [Manual]+++++++++++++++++++++++++++++++++++++++++++++++++ [1] @F_bar-@inv_bar-c_bar = 0; [2] betta*@R_bar-1 = 0; [3] betta*R_bar-1 = 0; [4] y_bar-@F_bar = 0; [1] c_bar = 1.0; [2] k_bar = 1.0; [3] y_bar = 1.0; [4] betta = 0.9; %Log-Linearized Model Equations++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variance-Covariance Matrix++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Sigma = [sigma_eps**2]; %End Of Model File+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++As one can see easily in this case, we are instructing the model to solve the 4 equation system in the four variables c_bar, k_bar, y_bar and betta. This is also a very common option to choose in order to obtain the model’s steady state efficiently and conveniently.
Option 4: Use the numerical root finder to solve for some steady states and get remaining ones residually¶
Option 4 is perhaps one of the most useful ways one can employ in order to obtain a DSGE model’s steady state solution as it focuses the numerical non-linear root-finding algorithm on a very small set of equations and unknown steady state variables, leaving the computation of the remaining steady state variables to be done separately and residually after the small set of steady state variables have been solved for. So using again a slightly tweaked version of the model file given in option 3 we could write this as:
%Model Description+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ This is just a standard RBC model, as you can see. %Model Information+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Name = Standard RBC Model; %Parameters++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ rho = 0.36; delta = 0.025; R_bar = 1.01; eta = 2.0; psi = 0.95; z_bar = 1.0; sigma_eps = 0.052; %Variable Vectors+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ [1] k(t):capital{endo}[log,bk] [2] c(t):consumption{con}[log,bk] [4] y(t):output{con}[log,bk] [5] z(t):eps(t):productivity{exo}[log,bk] [6] @inv(t):investment[log,bk] [7] @R(t):rrate %Boundary Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variable Substitution Non-Linear System++++++++++++++++++++++++++++++++++++++++++++++++ [1] @inv(t) = k(t)-(1-delta)*k(t-1); [2] @inv_bar = SS{@inv(t)}; [2] @F(t) = z(t)*k(t-1)**rho; [2] @Fk(t) = DIFF{@F(t),k(t-1)}; [2] @Fk_bar = SS{@Fk(t)}; [2] @F_bar = SS{@F(t)}; [3] @R(t) = 1+DIFF{@F(t),k(t-1)}-delta; [4] @R_bar = SS{@R(t)}; [3] @R(t+1) = FF_1{@R(t)}; [4] @U(t) = c(t)**(1-eta)/(1-eta); [5] @MU(t) = DIFF{@U(t),c(t)}; [5] @MU_bar = SS{@U(t)}; [6] @MU(t+1) = FF_1{@MU(t)}; %Non-Linear First-Order Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++ # Insert here the non-linear FOCs in format g(x)=0 [1] @F(t)-@inv(t)-c(t) = 0; [2] betta*(@MU(t+1)/@MU(t))*@R(t+1)-1 = 0; [3] @F(t)-y(t) = 0; [4] LOG(E(t)|z(t+1))-psi*LOG(z(t)) = 0; %Steady States [Closed Form]+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ [1] y_bar = @F_bar; %Steady State Non-Linear System [Manual]+++++++++++++++++++++++++++++++++++++++++++++++++ [1] @F_bar-@inv_bar-c_bar = 0; [2] betta*@R_bar-1 = 0; [3] betta*R_bar-1 = 0; [1] c_bar = 1.0; [2] k_bar = 1.0; [3] betta = 0.9; %Log-Linearized Model Equations++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variance-Covariance Matrix++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Sigma = [sigma_eps**2]; %End Of Model File+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++In this case we have simply taken the equation for y_bar outside of the section passed on to the non-linear root-finder and instead included it into the section for closed form steady state expressions. Whenever a model is instantiate like this, it first attempts to solve the smaller steady state system in the Manual section, before turning to the Closed Form section in which remaining steady states are computed residually based on the subset of steady states already solved numerically in the first step.
This is an extremely useful way of splitting down the problem, as many complex DSGE models often possess a large number of such residually determinable steady state values, while the core system on non-linear equations in a subset of steady states can be kept small in dimension and thus easier to solve. This really keeps the iteration burden on the non-linear solver to a minimum and often also allows the researcher to be less judicious in his choice of starting values leaving them at the generic default values. As a general rule, passing ever more complex and larger-dimensioned non-linear systems to the root-finding algorithm will decrease the chances of finding a solution easily, especially when simple generic starting values are employed. The issue of starting values take us straight to the next available option available to PyMacLab users.
Option 5: Use the numerical root finder to solve for steady states with pre-computed starting values¶
It is often useful and sometimes even outright necessary to supply the root-finding algorithm with pre-computed “intelligently” chosen initial starting values which are better than the generic choice of just passing a bunch of 1.0s to the system. To this end, whenever the list of generic starting values given in the numerical Manual section is a subset of the list of variable declarations in the closed form section, then the generic starting values automatically get replaced by the computed suggestions found in the Closed Form section. So an example of this would be:
%Model Description+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ This is just a standard RBC model, as you can see. %Model Information+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Name = Standard RBC Model; %Parameters++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ rho = 0.36; delta = 0.025; R_bar = 1.01; eta = 2.0; psi = 0.95; z_bar = 1.0; sigma_eps = 0.052; %Variable Vectors+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ [1] k(t):capital{endo}[log,bk] [2] c(t):consumption{con}[log,bk] [4] y(t):output{con}[log,bk] [5] z(t):eps(t):productivity{exo}[log,bk] [6] @inv(t):investment[log,bk] [7] @R(t):rrate %Boundary Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variable Substitution Non-Linear System++++++++++++++++++++++++++++++++++++++++++++++++ [1] @inv(t) = k(t)-(1-delta)*k(t-1); [2] @inv_bar = SS{@inv(t)}; [2] @F(t) = z(t)*k(t-1)**rho; [2] @Fk(t) = DIFF{@F(t),k(t-1)}; [2] @Fk_bar = SS{@Fk(t)}; [2] @F_bar = SS{@F(t)}; [3] @R(t) = 1+DIFF{@F(t),k(t-1)}-delta; [4] @R_bar = SS{@R(t)}; [3] @R(t+1) = FF_1{@R(t)}; [4] @U(t) = c(t)**(1-eta)/(1-eta); [5] @MU(t) = DIFF{@U(t),c(t)}; [5] @MU_bar = SS{@U(t)}; [6] @MU(t+1) = FF_1{@MU(t)}; %Non-Linear First-Order Conditions++++++++++++++++++++++++++++++++++++++++++++++++++++++ # Insert here the non-linear FOCs in format g(x)=0 [1] @F(t)-@inv(t)-c(t) = 0; [2] betta*(@MU(t+1)/@MU(t))*@R(t+1)-1 = 0; [3] @F(t)-y(t) = 0; [4] LOG(E(t)|z(t+1))-psi*LOG(z(t)) = 0; %Steady States [Closed Form]+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ [1] k_bar = 10.0; [2] y_bar = @F_bar; [3] c_bar = y_bar - delta*k_bar; [4] betta = 1/(1+@Fk_bar-delta); %Steady State Non-Linear System [Manual]+++++++++++++++++++++++++++++++++++++++++++++++++ [1] @F_bar-@inv_bar-c_bar = 0; [2] betta*@R_bar-1 = 0; [3] betta*R_bar-1 = 0; [4] y_bar-@F_bar = 0; [1] c_bar = 1.0; [2] k_bar = 1.0; [3] y_bar = 1.0; [3] betta = 0.9; %Log-Linearized Model Equations++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ None %Variance-Covariance Matrix++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ Sigma = [sigma_eps**2]; %End Of Model File+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++As is apparent, in this case the suggested values for the steady states given in the closed form section exactly mirror or overlap with the steady variables to be searched for using the non-linear root finder specified in the Manual section in the model file (which means that the latter is a subset of the former). Whenever this overlap is of the described subset-type, the values in the Closed Form section will always be interpreted as suggested starting values passed on to the non-linear root finder. Notice that in this case it is also possible to omit the additional specification of the generic starting values in the Manual section alltogether. However it is advisable to leave them there to give the program a better way of checking the overlap of the two sets of variables. Whenever they are omitted, this specific case of computing the steady state is triggered whenever the number of suggested starting values in the Closed Form section is exactly equal to the number of non-linear equations in the Manual section.
Option 6: Computing the steady state values dictionary entirely outside of PyMacLab and passing it¶
This is the most straightforward but at the same time possibly less “encapsulated” method of obtining the steady state of a model. In this case, we ignore everything inside the model file for the purpose of computing the steady state and instead do everything outside’ of the DSGE instance externally. When done we plug the values into a dictionary and pass it to the DSGE instance at instantiation time using the keyword pm.newMOD(modelfile,sstate=sstatedic). This method may only be necessary for extremely large models in which obtaining the steady state is a task so difficult that it may have to be dealt with in a separate programming block.
Option 7: Finding the steady state by only supplying information in the Closed Form section¶
This is the most straightforward but at the same time possibly also least-used method for finding a steady state and will not be explained in greater depth here. In this variant, the Manual section is marked as unused employing the “None” keyword and only information in the Closed Form section is provided. Since only the most simple DSGE models afford this option of finding the steady state, we will not discuss this option any further.
More about the steady state and its relevance to perturbation methods - A Detour¶
Perturbation methods discussed in the literature relevant to the discussion of solution methods for dynamic stochastic general equilibrium (DSGE) models are similar in spirit to Taylor series approximations of non-linear functions which are being taught to students in introductory/intermediate quantitative methods courses. Based on a functions derivatives, approximations are taken around a specific point or value of the parameter domain in order to approximate the fuction’s corresponding value when these values are perturbed away by small degrees from that point around which the approximation was taken.
This approach lends itself very well to the approximation of the exact solution of non-linear systems of expectatonal difference equations (i.e. DSGE models) chiefly because of two reasons. First of all, the assumption that shocks (perturbations) are not too large in some some in a real-world economic system is a reasonable one for most of the times. Secondly, while the general discussion of perturbation methods does not prescribe a preferred point around which the approximation should be taken, dynamic economic systems exhibting a steady state (equilibrium fixed point in the absence of any shocks) exhibit a perfect candidate value around which the approximation should be taken.
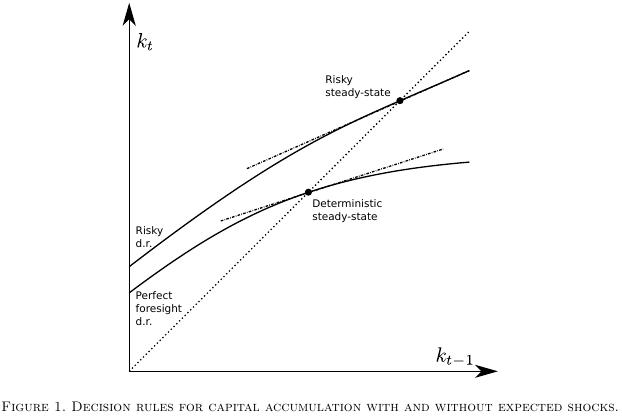
In the most recent literature [2] this point has however been given additional attention in that researchers typically consider two possible candidate steady state equilibrium points [2] around which to form the approximation. One of them is the traditional deterministic steady state to which the economic system gravitates when (all moments of) future shocks are assumed to be zero, while the other steady state, suitably called the risky or stochastic steady state is the one the system comes to rest to when agents populating the system know that future shocks will continue to occur based on some known (non-Knightian, if you like) distribution of those shocks.
Footnotes
| [1] | In other more complicated cases the law of motion of some exogenous shock process may depend on other endogenous states of the system. In this case we would probably want to pass the line to the non-linear root finder as its specification would influence the steady state value of other steady state variables. |
| [2] | Actually, there are more than 2 possible definitions of suitable steady state points. Here we want to draw attention to a stochastic point which has been defined as follows: “The risky steady-state is the point where agents choose to stay at a given date if they expect future risk and if the realization of shocks is 0 at this date.” (Coeurdacier, Rey and Winant, 2011) |
